Doctoral Research
Introduction : Motivation & Synopsis
Microstructural coarsening generally is observed in engineering materials during thermomechanical processes. The increase in the complexity of the microstructures with increasing the number of components and/or phases. With progressive in-situ experimental tools and a concomitant increase in the computational methods in the microstructural studies, open issues pertaining to self-similarity behavior on geometrical and topological features, concurrent grain growth and coarsening phenomena, the interplay between the components and phases during evolution is attempt in this thesis.
Numerical simulations, such as the phase-field approach can be used to explore the growth and/or coarsening of multi-component multi-phase polycrystalline materials. With the motivation to address the above mentioned phenomenon, the results of the present dissertation can be divided into two parts. In the first part, self-similar behavior on normal grain growth phenomena is elucidated in the form of short- and long-range grain size and topological correlations, effect of initial Voronoi filling in 2-D and 3-D microstructures. Further, the influence of pre-existing abnormal grains on transient grain growth behavior is investigated. The initial volume fraction of abnormal grains, grain size variation, mean distance between the grains are parameterized with more than hundred simulations. In the second part of the thesis, the effect of relative volume fraction, diffusivity and interfacial energy anisotropy in binary two-phase polycrystalline structures is studied. The simulations reveal the lowest growth kinetics for equivolume fraction systems. In addition, the microstructural patterns depending on the energy ratio between grain boundary and inter-phase boundary are demonstrated. Finally, suppressed microstructural coarsening phenomena is obtained for ternary three-phase polycrystalline microstructures. Various local morphological features are reported during the evolution processes. The extended abstract of the each chapter results presented below.
Formation of first-neighbor topological clusters during the isotropic grain growth
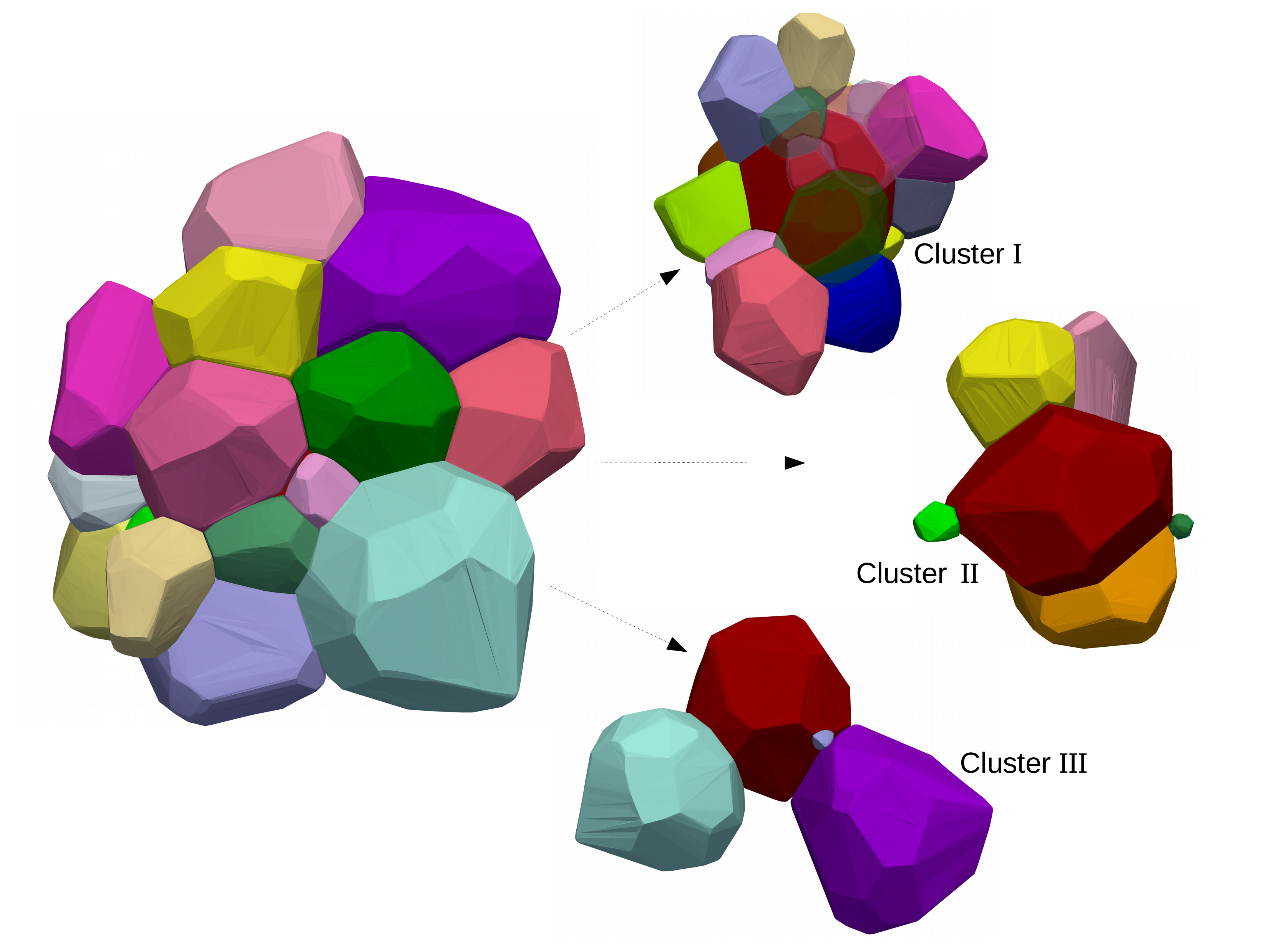
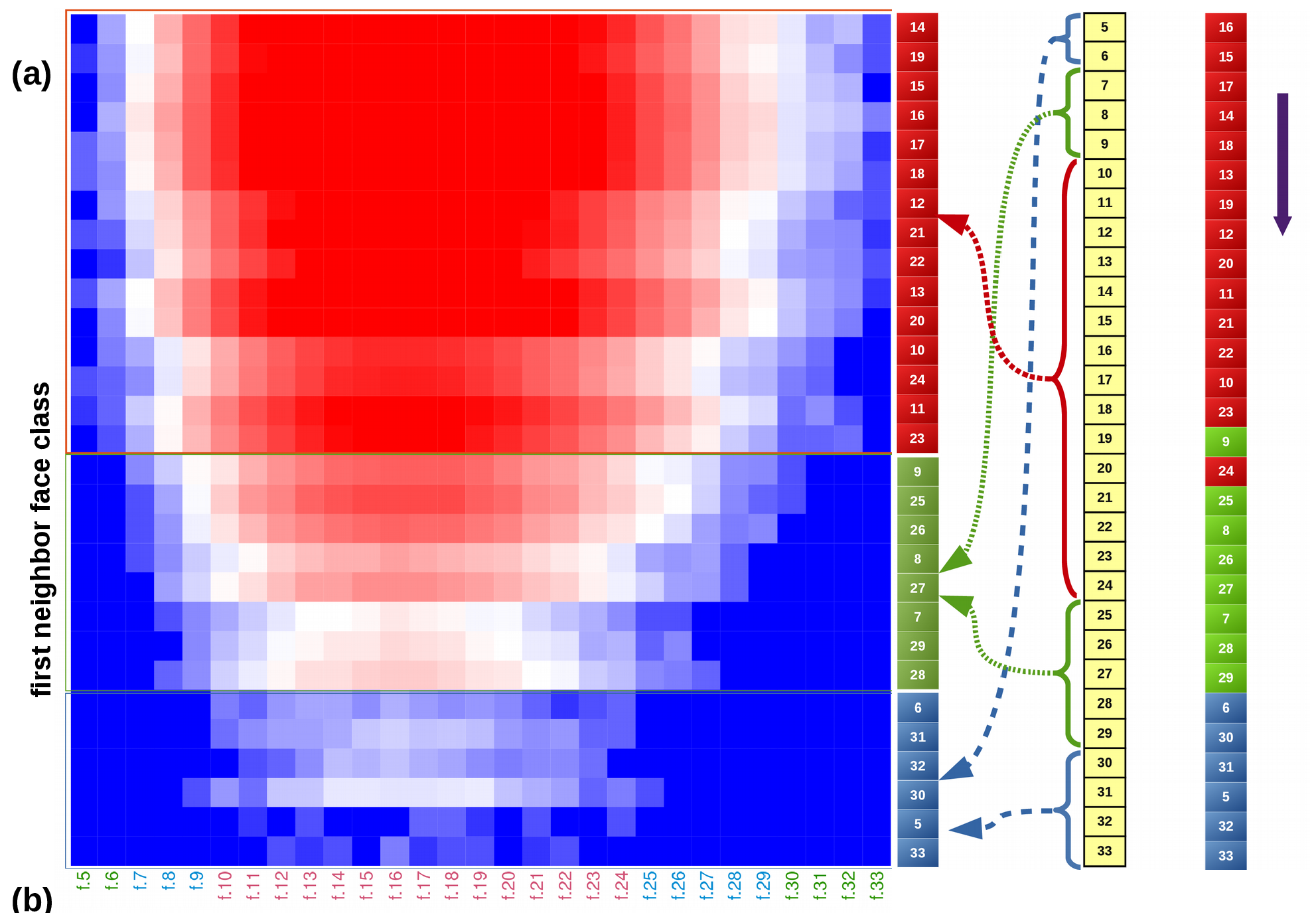
Grain growth in polycrystalline material is influenced by numerous factors which convolute the understanding of the process. Present work intends to delineate certain aspects of this complexity by quantitatively analyzing the topological evolution of the grains and its first-neighbors resulting from multiphase-field simulations. Upon verifying the consistency of this approach with the existing 2- and 3- dimensional analytical predictions, face-switching events of about 75000 grains in 3-D domain is extensively analyzed. Despite the expected numerical dominance of the face-loss event, we find the affinity of this event to decrease with increase in face-class. A transition in switching affinity is observed above face-class 14, wherein, the face-gain events are preferred over loss events. The pathway of the topological evolution is comprehensively analyzed to identify its influence on the life-span of the grains. This analysis indicates that the topological evolution around the average face-class, dead zone, invariably shortens the life-span of the grains and considerable gain in the face-class is seldom observed. The topological behavior of the first-neighbors during grain growth is quantitatively captured through a well-known statistical tool called heat-maps. And for the first time, the formation of topological clusterswhich account for the time-invariant behavior of the grains is elucidated. The results presented in the chapter has been published in Computational Materials Science (2017).
Grain size and topological correlations on normal grain growth
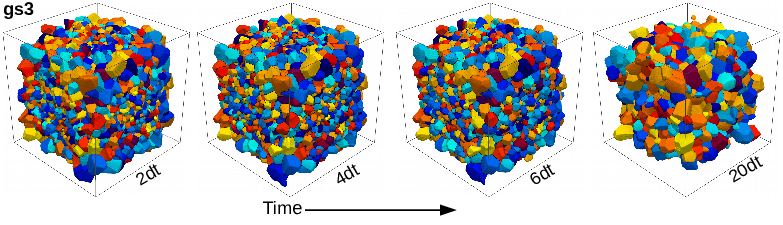
Since the analytical grain growth models hold many simplified assumptions, the experiments and simulation results often differ from classical theories. In this chapter, the phase field simulations attempt to elucidate some of the open questions, concerning the self-similarity and correlation behavior of the 2-D and 3-D microstructures. The validity of Hillert’s linear growth law assumption, based on mean curvature, is addressed. Furthermore, the role of the dimensionality effect has been observed during growth. The self-similar state has been characterized by the geometrical and topological features of the microstructure. The short- and long-range neighbor grain size and topological correlation behavior in 2-D have been validated and extended to 3-D microstructures. It is found that the correlation of the short-range neighbors is much more significant than the long-range interactions. Accomplishing a quasi-steady state regime in the isotropic growth case is roughly independent of the initial grain arrangements.
Transient phenomena induced by abnormallylarge grains during 2-dimensional isotropic grain growth.
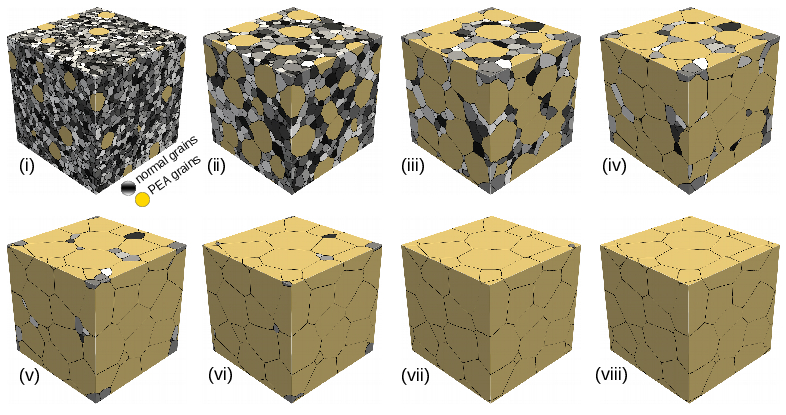
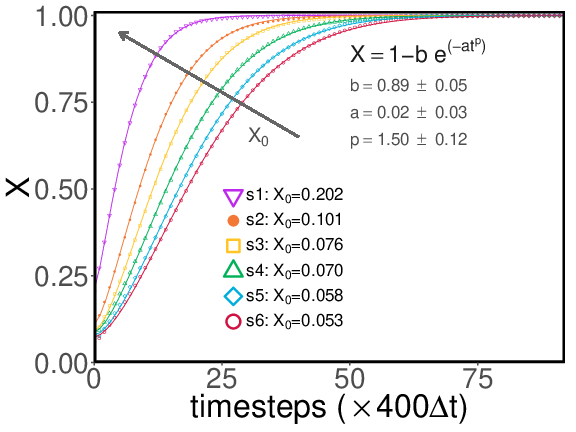
Abnormallylarge grains, whose sizes are greater than twice the critical radius (2Rc), are known to alter the isotropic grain growth phenomena. In the present work, phase-field simulations of 2-dimensional microstructures are extensively analyzed to elucidate the deviations from the normal grain growth introduced by the presence of abnormal grains. Polycrystalline microstructures that are artificiallymade to resemble physical structures, by governing the distribution and the sizes of the abnormal grains, is employed to analyse the grain growth in the presence of large grains. This study unravels that the abnormal grains induce a period of transition during which its grain size distribution is shifted and confined within 2Rc, indicating a complete disappearance of the abnormality in the microstructure. Furthermore, it is identified that this transition period establishes a bimodal distribution, which subsequently evolves into a unimodal time-invariant distribution. This behaviour noticeably reveals the misconception that the disappearance of the abnormality signifies the onset of normal grain growth. Moreover, despite the apparent disappearance of the abnormal grains, a continued increase in the volume-fraction of these pre-existingabnormal grains is recognized, and in the steady-state condition, it is observed that the microstructure predominantly consists of these pre-existing abnormal grains. Influence of the factors like initial volume-fraction of the abnormal grains Fo and degree of abnormality ¯Umax on the duration of the transient period is quantified by investigating close to hundred microstructures with unique Fo and ¯Umax. The results presented in the chapter has been published in Computational Materials Science (2018).
Concurrent grain growth and coarsening of binary two-phase microstructures
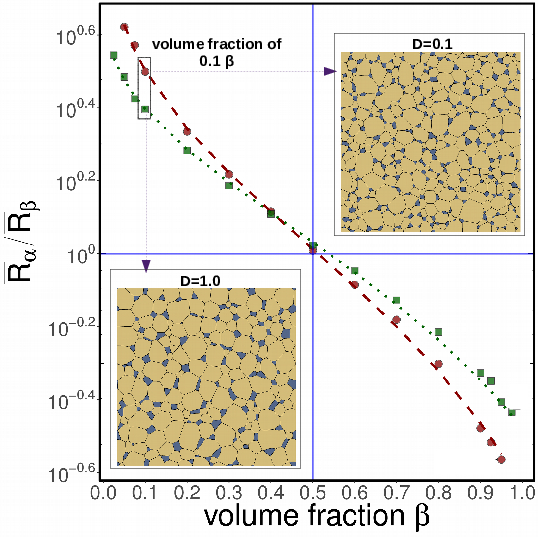
A phase-field model is exploited to demonstrate the influence of relative volume fractions and bulk diffusivity on the grain growth phenomena in two-phase polycrystalline systems. For very small and high volume fractions, the simulated morphology consists of a dispersion of isolated minor phase grains embedded in the matrix of major phase grains. At intermediate fractions, the obtained microstructure resembles an interpenetrating network-like structure. The performed large-scale 2-D simulations elucidate the governing mechanisms for the concurrent two-phase growth at low and high volume fractions, and the continuous transition between interface-controlled and diffusion-limited regimes. While the slowest kinetics is observed for the 0.5α−0.5β volume fraction case, irrespective of the diffusivity, the fastest kinetics is displayed by the pure systems, with a slight difference, which is due to relative interfacial energies. The relative growth rates of the individual phases and the maximum attainable grain size to mean size ratio are observed to follow the well-known trends for isotropic systems. The obtained results for the concurrent growth of a minor phase with various diffusivities, reveal that it is difficult to reconcile all observed behaviors with a universal Zener relation, in contradiction to the previously made claims in the literature. The results presented in the chapter has been published in Computational Materials Science (2019).

Microstructural coarsening of equivolume fraction duplex materials
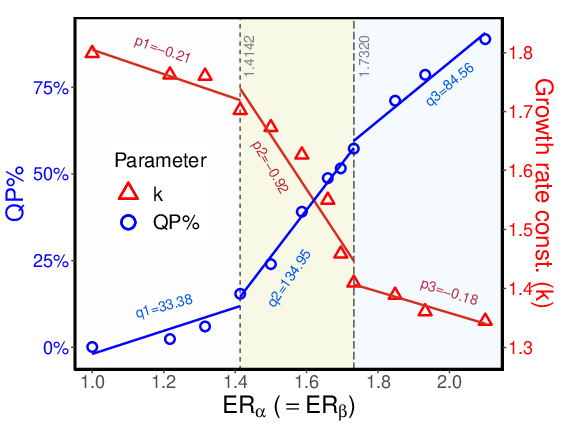
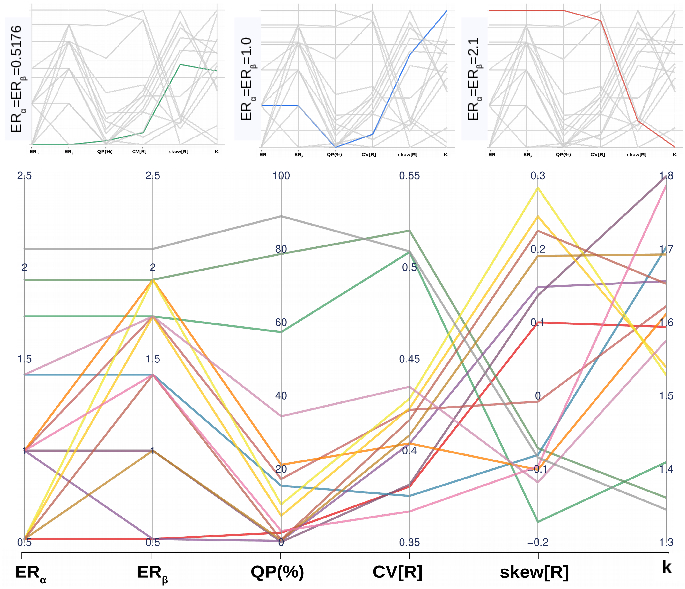
A multi-phase field model is employed to study the microstructural coarsening of 0.5α−0.5β system with wide range of interfacial energy ratio (ERα=σαiαjσαβ and ERβ=σβiβjσαβ) combinations. The aim has been to cover the full range of microstructures observed in the nonconserved (NCS) and conserved systems (CS). The mechanisms of formation of the complex microstructures and the characteristic individual phase morphologies have been briefly discussed. Besides, four interface energy regime criteria were proposed to describe the predicted microstructural features. The mean grain size evolution elucidate that the governing mechanisms for NCS and CS are interface-controlled and bulk diffusion-limited coarsening mechanisms respectively. The stable quadruple junctions over the triple junctions can be seen for some higher energy ratio cases. It is difficult to reconcile all observed two-phase GSD with single-phase analytical models. Additionally, statistical parameters have been exploited to evolute the GSD. The relative growth rates of the individual phases are nearly identical, irrespective of the varying interfacial energy ratios used. The parallel-coordinate plot is introduced to consolidate the results and proposed to design the duplex microstructures with the required properties.
Microstructural coarsening of ternary two and three-phase polycrystalline materials
A thermodynamically consistent phase-field model is exploited to demonstrate the influence of relative volume fractions on the microstructural coarsening of complex polycrystalline systems. The performed two-dimensional mean grain size data are found to follow the power growth law kinetics with the growth coefficient in the range of 3<m<4 depending on process parameters. While the slowest kinetics is perceived for the 0.33α−0.33β−0.33γ volume fraction case, the fastest kinetics is exhibited by the pure systems. The transition between interface-controlled and diffusion-limited regimes ascertains the individual phase coarsening. As the volume fraction decreases for the particular phase, the intergrain distance increases and long-range diffusion slows down the coarsening. In the domain, cooperative diffusion of multicomponent elements further suppresses the grain growth. At intermediate volume fractions, the obtained grain size distribution is more closely approximated by the Weibull function than by the Hillert distribution. The relative growth rates of the individual phases and the maximum attainable grain size to mean size ratio follow the isotropic growth behavior. It is difficult to reconcile the concurrent coarsening of minor constituents with a universal Zener relation, provided that an empirical Zener relation, like the formulation for a three-phase system with a low volume fraction, is proposed.
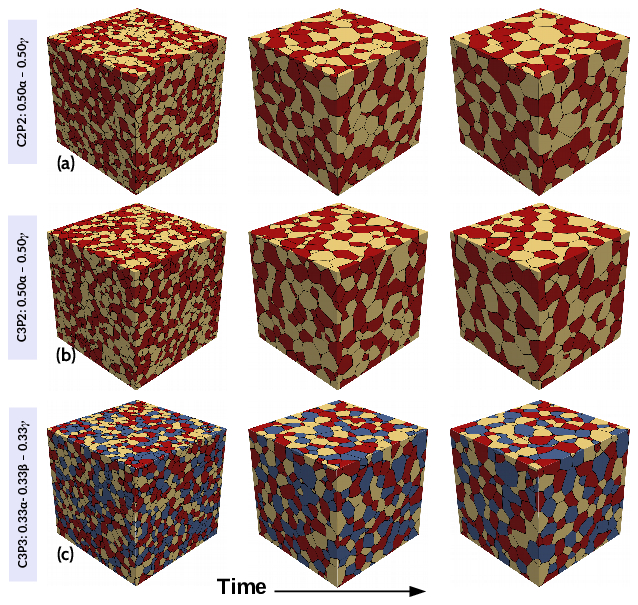
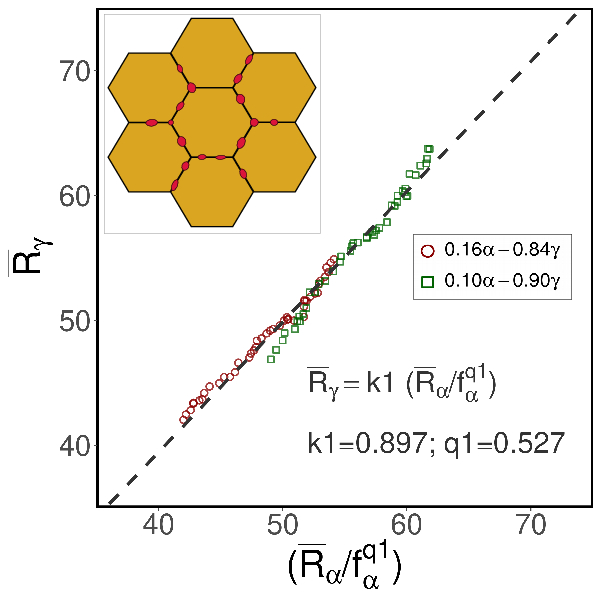
This research work not only contributes to the advancement of our understanding of microstructural coarsening in bulk polycrystalline structures but provides a general framework in phase-field models, illustrate the applicability to examine other physical phenomenon in materials science such as thin-films, multi-layers etc.