Mathematical models for predicting microstructural evolution
Research Overview
My research focus is on the microstructural coarsening of multicomponent multiphase polycrystalline materials during thermo-mechanical processes in the interdisciplinary areas of materials engineering. During my graduate studies (doctoral), I have been involved with the development of phase-field models and data-analytical tools to study several metallic/ceramic microstructural evolution processes. In particular, my doctoral dissertation (KIT, Germany) examines the underlying mechanisms responsible for grain coarsening in complex polycrystalline systems through large-scale 2-D and 3-D simulations. Besides, a considerable part of the thesis also explores the statistical quantification of the developing microstructures and their influence on growth phenomena using statistical tools like R. Before my doctoral research, I obtained my masters from IIT Madras, India in the area of specialization materials engineering.
Multi-Phase-field model
Microstructural evolution is thermodynamically driven by the minimization of free energy. Phase-field models: Implicit tracking of the interface movement is obtained through the formulation of partial differential equations. Bulk-free energy functions, related to specific material systems, can be derived from physical principles or can be computed from thermodynamic databases (CALPHAD).
Microstructural evolution of complex polycrystalline system ⇒ grand-potential formulation, Ω(T,μ,ϕ)=∫V(Ψ(T,μ,ϕ)+ϵa(ϕ,∇ϕ)+1ϵw(ϕ))dV
The gradient energy density,
a(ϕ,∇ϕ)=∑m<nσmn[amn(qmn)]2|qmn|2
qmn=ϕm∇ϕn−ϕn∇ϕm.
Multi-obstacle potential including higher order terms:
w(ϕ)=16π2∑m<nσmnϕmϕn+∑m<nσmnoϕmϕnϕo
Interpolation of the individual grand potential densities
Ψ(T,μ,ϕ)=N∑α=1Ψα(T,μ)h(ϕα)
Ψα(T,μ)=fα(cα(μ),T)−K−1∑i=1μicαi(ϕ,T)
Binary two-phase system
The chemical energies of the respective phases are constructed using the parabolic type of functions: fα=Aα(c−cαeq)2
fβ=Bβ(c−cβeq)2,
The interpolated free energy as, f(ϕ,c)=fαh(ϕα)+fβh(ϕβ),
and where the coefficients of Aα and Bβ can be used to determine the steepness of the parabolic free energy. cαeq and cβeq are the equilibrium compositions of the α and β phase. \ The phase compositions will not deviate much from the equilibrium phase compositions in bulk materials.
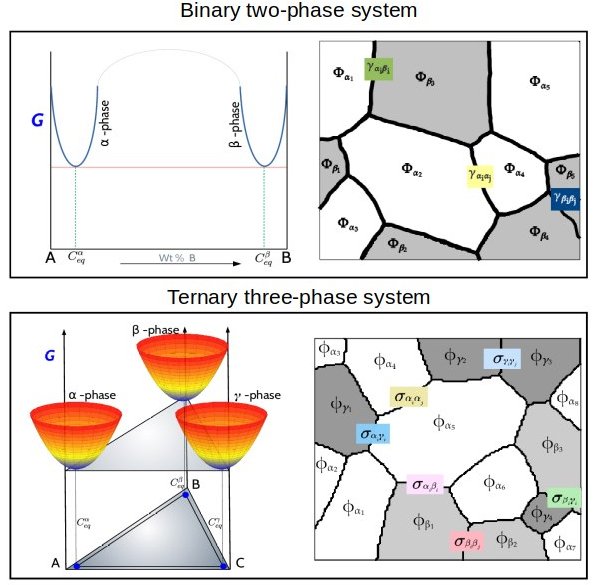
Ternary three-phase system
Three-phase polycrystalline structure which consists of a number of N(=Nα+Nβ+Nγ), α, β and γ phase grains with different orientations. The chemical energies of the respective phases are constructed using the paraboloid type of functions:
where, fα(cA,cB,cC)=˜Aαc2A+˜Bαc2B+˜Cαc2C+˜DαcAcB+˜EαcBcC+˜FαcCcA+˜GαcA+˜HαcB+˜IαcC+˜Jα,
The ˜A, ˜B, ˜C, ˜D, ˜E, ˜F, ˜G, ˜H, ˜I and ˜J are the components at specific temperature. Taking the constraint cA+cB+cC=1, we can rearrange the above equation as follows. fα=Aα(cA−ceqAα)2+Bα(cB−ceqBα)2+Cα[(cA−ceqAα)(cB−ceqBα)]+Dα
where cA, cB, cC are the concentrations of A, B, and C, respectively.
The interpolated free energy as, f(ϕ,c)=fαh(ϕα)+fβh(ϕβ)+fγh(ϕγ),
Phase-field model (cont.)
The evolution equation for the conserved concentration fields can be expressed as follows: ∂ci∂t=∇⋅(K−1∑j=1Mij(ϕ)∇μj).
Here, Mij(ϕ) is the mobility of the interface, formulated as follows by an interpolation of the individual phase mobilities: Mij(ϕ)=N−1∑α=1Mαijgα(ϕ).
Mαij=Dαij(∂cαi(μ,T)∂μj).
The evolution equation for the nonconserved N phase-field variables (ϕm,m=1,....,N) can be written as τϵ∂ϕm∂t=ϵ[∇⋅∂a(ϕ,∇ϕ)∂∇ϕm−∂a(ϕ,∇ϕ)∂ϕm]−1ϵ∂w(ϕ)∂ϕm−∂Ψ(T,μ,ϕ)∂ϕm−λ.
Simulation set-up
The distribution of grains, in both 2D and 3D simulations, is implemented by a Voronoi algorithm wherein the points corresponding to the grains are randomly placed in the domain and allowed to initialize. A 3D representation of the final arrangements of the grains obtained by this algorithm is shown in the above Figure. In order to render an indicative statistical study, domains of sizes 4000×4000 and 512×512×512 gridpoints with 60000 and 75000 grains are analysed in 2D and 3D, respectively. $ The variational derivative of the functional, F with respect to the phase-field variable ϕα and phase-field gradient ∇ ϕα generates scalar and vector respectively. Thus, an appropriate numerical scheme is adopted to optimize the evaluation . The evolution equation is discretized in an equidistant grid of cell sizes, Δx=Δy=Δz =1.0 by a finite difference method. A consistency within the simulations is attained by fixing the length scale of the diffuse interface width to ϵ= 4Δx. Furthermore, simulations are made computationally efficient by implementing a which restricts the number of order parameters solved at each grid point.